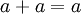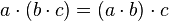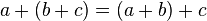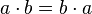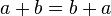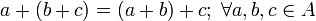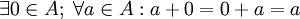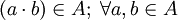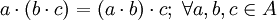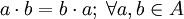2.4 MAPAS DE KARNAUGH DE 5 VARIABLES

Recordemos que para conseguir el mapa de 5 variables, debe proyectarse el mapa de 4 variables. El abatimiento es hacia la derecha ya que el número de variables es impar. La figura adjunta muestra la proyección del mapa de 4 variables.

Obsérvese que al mapa que se proyecta se le antepone un 0 y al proyectado un 1. También, se ha asociado a cada celda el número binario correspondiente, el cual se obtuvo asignando el valor binario a cada variable en dicha celda.

Sustituyendo el número binario de cada celda por su equivalente decimal, se obtiene el mapa de Karnaugh para 5 variables que se empleará para minimizar funciones de conmutación de 5 variables independientes . La figura adjunta presenta este mapa.

Para generar el código de Gray para 5 variables, se traza la greca de Gray sobre el mapa K para 5 variables y se escribe el código binario asociado a cada celda.

La figura adjunta muestra la greca de Gray sobre el mapa de Karnaugh de 5 variables.

A continuación se presentan algunos ejemplos que muestran la aplicación del mapa para la minimización de funciones de conmutación de 5 variables binarias.

EJEMPLO 6. Minimice las siguientes funciones, empleando el método de Karnaugh:

F1 = Sumaminitérminos (0,1,3,8,9,11,16-17,19,24,25,29-31)

F2 = Sumaminitérminos (0-4,6,9,10,15-20,22,23,25,26,31)

SOLUCION

Las siguientes figuras presentan los mapas K para F1 y F2:

MÉTODO DE REDUCCIÓN DE MAPAS DE KARNAUGH

El Álgebra de Boole, resuelve problemas que dependiendo del número de términos que tenía la función canónica, siendo el número de compuertas lógicas utilizadas igual al número de términos obtenidos MÁS UNO; por lo tanto, los circuitos obtenidos son de dos niveles de conmutación con un tiempo mínimo de retardo, pero que de ninguna manera es el más sencillo ni el más económico .

2.1 Generación de MAPA DE KARNAUGH de 2 y 3 variables.

Los mapas de Karnaugh es uno de los métodos más prácticos. Se puede decir que es el más poderoso, cuando el número de variables de entrada es menor o igual a seis; más allá, ya no es tan práctico. En general, el mapa de Karnaugh se considera como la forma gráfica de una tabla de verdad o como una extensión del diagrama de Venn.

Antes de explicar como se utiliza el mapa de Karnaugh en la minimización de funciones, veremos como se obtiene el mapa. Esto nace de la representación geométrica de los números binarios . Un número binario de n bits, puede representarse por lo que se denomina un punto en un espacio N. Para entender lo que se quiere decir con esto, considérese el conjunto de los números binarios de un bit, es decir 0 o 1. Este conjunto puede representarse por dos puntos en un espacio 1; esto es, por dos puntos unidos por una línea. Tal representación se denomina un cubo 1.

De la Figura 2.1, se observa que el cubo 1 se obtuvo proyectando al cubo 0 y que el cubo 2 se obtendrá proyectando al cubo 1.

De la Figura 2.2, se observa que al reflejarse el cubo 1 se obtiene un cuadrilátero cuyos vértices representan un número binario. Estos números se obtienen al agregar un 0 a la izquierda de los vértices del cubo reflejado. Del cubo 2 se observa que se obtienen 4 vértices, los cuales corresponden a las combinaciones de dos variables (22=4), pero si se sigue la trayectoria indicada en la Figura 2.2.b, se podrá observar que al pasar de un vértice al otro, existe un solo cambio , lo que da lugar a un código especial , debido que a no sigue la formación del código binario, como se muestra en la siguiente tabla. Más adelante le daremos un nombre a este código.

A	B
0	0
0	1
1	1
1	0

Ahora, si a cada vértice del cubo 2 se le asigna un casillero, se tendrá la Figura 2.3.

De la Figura 2.3.(b), si proyectamos el cubo 2, obtendremos el cubo 3, el cual se muestra en la Figura 2.4.

De la Figura 2.4.b, si seguimos la trayectoria marcada por las flechas obtendremos la siguiente tabla, en donde de un carácter a otro existe un solo cambio; otra característica de la tabla, es el reflejo que existe entre los caracteres 1-2 y 5-6 de la columna C y el reflejo entre los caracteres 2-3-4-5 en la columna B. El reflejo que existe siempre es con respecto al eje central de simetría.

Ahora que tenemos el cubo 3, podemos obtener la representación en la forma de la Figura 2.3.(a), (b) y (c), lo cual se muestra en la Figura 2.5.

El levantamiento del cubo 3, a partir de la Figura 2.5, se muestra en la Figura 2.6.

Ahora, si asignamos una área a cada punto, como se muestra en la Figura 2.7, se obtendrá la representación que se denomina mapa del cubo N, que en este caso fue desarrollado para un cubo 3. Como se tienen 8 casilleros, éstos corresponden a las combinaciones de tres variables, la cuales pueden ser A, B y C, siendo A la más significativa y C la menos significativa, por lo que la tabla funcional para presentar este mapa es:

DEC	CÓDIGO
	BINARIO				GRAY
	A	B	C		G1	G2	G3
0 1 2 3 4 5 6 7	0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1		0 0 0 0 1 1 1 1	0 0 1 1 1 1 0 0	0 1 1 0 0 1 1 0

La primera tabla corresponde al código binario y la otra corresponde al código especial que en realidad se le conoce como código de Gray o código reflejado. Como veremos, ambos códigos están implícitos en el mapa de Karnaugh.

Si observamos el mapa de la Figura 2.8.(d), cada casillero tiene asignado un número, el cual corresponde a un número del código binario. De la misma figura pero del inciso (e), si seguimos la trayectoria marcada por las flechas, cada número representa a un carácter del código Gray.

En la tabla anterior, se muestran cada uno de los códigos mencionados.

Operaciones básicas

Después de valores, el ingrediente siguiente de cualquier sistema algebraico es sus operaciones. Mientras que es elemental la álgebra se basa en la multiplicación numérica de las operaciones xy, adición x + y, y − de la negaciónx, La álgebra boleana se basa acostumbradamente en las contrapartes lógicas a esas operaciones, a saber conjunción x∧y (Y), separación x∨y (O), y ¬ del complemento o de la negaciónx (NO). En la electrónica, Y se representa como multiplicación, O se representa como adición, y NO se representa con un overbar: x ∧ y y x ∨ y, por lo tanto, conviértase xy y x + y.

La conjunción está la más cercana de estos tres a sus contrapartes numéricas, de hecho en 0 y 1 él es multiplicación. Pues una operación lógica la conjunción de dos asuntos es verdad cuando ambos asuntos son verdades, y de otra manera son falsa. La primera columna del cuadro 1 abajo tabula los valores de x∧y para las cuatro valuaciones posibles para x y y; tal tabulación tradicionalmente se llama a tabla de verdad.

La separación, en la segunda columna de las figuras, trabajos casi tiene gusto de la adición, con una excepción: la separación de 1 y 1 es ni 2 ni 0 pero 1. Así la separación de dos asuntos es falsa cuando ambos asuntos son falsos, y es de otra manera verdad. Esto es justo la definición de la conjunción con verdad y falso intercambiados por todas partes; debido a esto decimos que la separación es dual de la conjunción.

La negación lógica sin embargo no trabaja como la negación numérica en todos. En lugar corresponde al aumento: ¬x = x+1 MOD 2. Con todo comparte en común con negación numérica la característica que la aplicación de ella vuelve dos veces el valor original: ¬¬x = x, apenas como − (−x) = x. Una operación con esta característica se llama involución. El sistema {0.1} tiene dos permutaciones, ambos involutary, a saber la identidad, ningún movimiento, correspondiendo a MOD numérica 2 de la negación (desde +1 = −1 MOD 2), y al INTERCAMBIO, correspondiendo a la negación lógica. Usando la negación podemos formalizar la noción que la conjunción es dual a la separación vía Leyes de De Morgan, ¬(x∧y) = ¬x ∨ ¬y y ¬ (x∨y) = ¬x ∧ ¬y. Éstos se pueden también interpretar como definiciones de la conjunción en términos de separación y viceversa: x∧y = ¬(¬x ∨ ¬y) y x∨y = ¬(¬x ∧ ¬y).

El cuadro 2 demuestra los símbolos usados adentro electrónica digital para la conjunción y la separación; los puertos de la entrada están a la izquierda y las señales atraviesan al puerto de salida a la derecha. Los inversores que niegan las señales de entrada en la manera adentro, o las señales de salida en la salida, se representan como los círculos en el puerto que se invertirá.

Operaciones derivadas

Otras operaciones boleanas son derivable de éstos por la composición. Por ejemplo implicación x→y (IMP), en la tercera columna de las figuras, está una operación binaria que es falsa cuando x es verdad y y es falso, y verdad de otra manera. Puede ser expresado como x→y = ¬x∨y (el OR-gate del cuadro 2 con x entrada invertida), o equivalente ¬ (x∧¬y) (su De Morgan equivalente en el cuadro 3). En lógica se llama esta operación implicación material, para distinguirlo de conceptos lógicos relacionados pero no-Boleanos tales como entailment e implicación relevante. La idea es que una implicación x→y está por el defecto verdad (el valor de verdad más débil en el sentido que falso implica verdad pero no viceversa) a menos que su premisa o antecedente x sostiene, en este caso la verdad de la implicación es la de su conclusión o consiguiente y.

Aunque la separación no es las contrapartes exactas de la adición numérica, la álgebra boleana no obstante tiene contrapartes exactas, llamadas exclusivo-o (XOR) o paridad, x⊕y. Según las indicaciones de la cuarta columna de las figuras, exclusivo-o de dos asuntos es verdad en el momento en que uno de los asuntos es exactamente verdad; equivalente cuando un número impar de los asuntos es verdad, de dónde la “paridad conocida”. Exclusivo-o es la operación de MOD 2 de la adición. Exclusivo-o de cualquier valor con sí mismo desaparece, x⊕x = 0, puesto que las discusiones tienen un número par de cualquier valor x tiene. Su símbolo de la electrónica digital se demuestra en el cuadro 2, siendo un híbrido del símbolo de la separación y del símbolo de la igualdad. El último refleja el hecho de que la negación (que es también la dual) de XOR, el ¬ (x⊕y), es la equivalencia lógica, EQV, siendo verdad en el momento en que x y y es el igual, verdad o ambos falsos. XOR y EQV son las únicas operaciones boleanas binarias que son comutativas y que tablas de verdad tienen igualmente mucho 0s y 1s. Exclusivo-o junto con la conjunción constituya otra base completa para la álgebra boleana, con las operaciones boleanas reformuladas como Polinomios de Zhegalkin.

Otro ejemplo es movimiento de Sheffer, x|y, NAND puerta adentro electrónica digital, que es falso cuando ambas discusiones son verdades, y verdad de otra manera. El NAND es definible por la composición de la negación con la conjunción como x |y = ¬(x∧y). No tiene su propio símbolo esquemático mientras que se representa fácilmente como Y puerta con una salida invertida. Desemejante de la conjunción y de la separación, el NAND es una operación binaria que se puede utilizar para obtener la negación, vía el ¬ de la definiciónx = x|x. Con la negación a disposición uno puede entonces alternadamente definir la conjunción en términos de NAND vía x∧y = ¬(x|y), de que el resto de las operaciones boleanas del arity distinto a cero pueden entonces ser obtenidas. NI, ¬ (x∨y), como el dual evidente del NAND responde a este propósito igualmente bien. Este carácter universal del NAND y NI les hace una opción popular para órdenes de puerta, circuitos integrados con las puertas de uso general múltiples.

La dualidad antedicha de la conjunción y de la separación es expuesta más lejos por los leyes de De Morgan, ¬ (x∧y) = ¬x∨¬y y ¬ (x∨y) = ¬x∧¬y. El cuadro 3 ilustra los leyes de De Morgan dando para cada puerta a su De Morgan dual, convertido de nuevo a la operación original con los inversores en entradas y las salidas. En el caso de la implicación, tomando la forma de un OR-gate con un inversor en la separación, que el inversor es cancelado por el segundo inversor que habría ido allí. El De Morgan dual de XOR es XOR justo con un inversor en la salida (no hay símbolo separado); como con la implicación, poniendo los inversores en las tres cancelaciones de los puertos el inversor dual de la salida. Más generalmente, cambiar un número impar de inversores en una puerta de XOR produce la puerta dual, un número par deja la funcionalidad de la puerta sin cambios.

Como con todos los otros leyes en esta sección, Leyes de De Morgan puede ser verificado caso por caso para cada uno de los 2ⁿ valuaciones posibles del n variables que ocurren en la ley, aquí dos variables y por lo tanto 2² = 4 valuaciones. Los leyes de De Morgan desempeñan un papel en poner términos boleanos en ciertas formas normales, una de las cuales nosotros encontrará más adelante en la sección en validez y lo completo.

El cuadro 4 ilustra corresponder Diagramas de Venn para cada uno de las cuatro operaciones presentó en cuadros 1-3. El interior (respectivamente el exterior) de cada círculo representa el valor verdad (respectivamente falso) para la entrada correspondiente, x o y. La convención seguida aquí es representar el verdad o las salidas 1 como regiones oscuras y el falso como luz, pero utilizan a la convención reversa también a veces.

Todas las operaciones boleanas

Hay infinitamente muchas expresiones que se pueden construir a partir de dos variables usando las operaciones antedichas, sugiriendo gran expresividad. Con todo una discusión de cuenta directa demuestra que solamente 16 operaciones binarias distintas en dos valores son posibles. Cualquier operación binaria dada es determinada completamente por sus valores de la salida para cada combinación posible de los valores de la entrada. Las dos discusiones tienen 2 × 2 = 4 las combinaciones posibles de valores entre ellos, y allí son 2⁴ = 16 maneras de asignar un valor de la salida a cada uno de estos cuatro valores entrados. La opción de una de estas 16 asignaciones entonces determina la operación; tan todas juntas allí son solamente 16 operaciones binarias distintas.

Las 16 operaciones boleanas binarias pueden ser organizadas como sigue:

Dos operaciones constantes, 0 y 1.

Cuatro operaciones dependientes en una variable, a saber x, ¬x, y, y ¬y, que tablas de verdad ascienden a dos juxtaposed los rectángulos, uno que contenía dos 1s y los otros dos 0s.

Dos operaciones con una tabla de verdad del “tablero de damas”, a saber XOR y EQV.

Cuatro operaciones se obtienen de la separación con un cierto subconjunto de sus entradas negadas, a saber x∨y, x→y, y→x, y x|y; sus tablas de verdad contienen un solo 0.

Los cuatro finales vienen del mismo tratamiento aplicado a la conjunción, teniendo un solo 1 en sus tablas de verdad.

10 de las 16 operaciones dependen de ambas variables; todos son representables esquemáticamente como una Y-puerta, un OR-gate, o XOR-puerta, con un puerto invertido opcionalmente. Para Y y O las puertas la localización de cada inversor importa, porque la puerta de XOR que no lo hace, sólo si haya un número uniforme o impar de inversores.

Operaciones de otra arities sea posible. Por ejemplo las contrapartes ternarias de la separación se pueden obtener como (x∨y)∨z. En general n- operación ary, una que tiene n las entradas, tienen 2ⁿ valuaciones posibles de esas entradas. Una operación tiene dos posibilidades de cada uno de éstos, de dónde existen 2²ⁿ n- operaciones boleanas ary. Por ejemplo, hay 2³² = 4.294.967.296 operaciones con 5 entradas.

Aunque la álgebra boleana confina la atención a las operaciones que vuelven un de un solo bit, el concepto generaliza a las operaciones que toman n pedacitos adentro y vuelta m pedacitos en vez de un pedacito. Los diseñadores del circuito de Digital dibujan las operaciones tales como las cajas convenientemente formadas con n alambres que entran a la izquierda y m alambres que salen a la derecha. Tales operaciones multi-output se pueden entender simplemente como m n- operaciones ary. La cuenta de la operación se debe entonces levantar a m- energía del th, o, en el caso de n entradas, (2²ⁿ)^m = 2^m2n operaciones. El número de operaciones boleanas de esta clase generalizada con las entradas de la opinión 5 y 5 salidas es el × 1.46 10⁴⁸. Un módulo de la puerta o de la computadora de la lógica traz 32 pedacitos a 32 pedacitos podía poner cualquiera en ejecución 5.47 del × 10^{41.373.247.567} operaciones, más que es obtenido ajustando a googol 28 veces.

Álgebra de Boole

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Álgebra de Boole (también llamada Retículas booleanas) en informática y matemática, es una estructura algebraica que rigorizan las operaciones lógicas Y, O y NO, así como el conjunto de operaciones unión, intersección y complemento.

Definición

El Álgebra de Boole es una estructura algebraica que puede ser considerada desde distintos puntos de vista matemático Como retículo

El álgebra de Boole es un retículo (A, 1,0, , +), donde el conjunto A = {1,0}, como retículo presenta las siguientes propiedades, las leyes principales son estas:

1. Ley de Idempotencia:

2. Ley de Asociatividad:

3. Ley de Conmutatividad:

4. Ley de Cancelativo

Como anillo

El Álgebra de Boole tiene Estructura algebraica de Anillo:

Grupo abeliano respecto a (+)

El conjunto A es un Grupo abeliano respecto a (+):

1. (+) es una operación interna en A:

2. Es asociativa:

3. Tiene elemento neutro

4. Tiene elemento simétrico:

5. es conmutati Grupo abeliano respecto a (·)

El conjunto A es un Grupo abeliano respecto a ():

6. () es una operación interna en A:

7. Es asociativa:

8. Tiene elemento neutro

9. Tiene elemento simétrico:

10. es conmutativa:

El conjunto A={0,1} es un Grupo abeliano respecto a ():

6. () es una operación interna en A:

7. Es asociativa:

8. Tiene elemento neutro

9. Tiene elemento simétrico:

10. es conmutativa:

OPERACIONES LOGICAS:

Combinando proposiciones simples obtenemos proposiciones compuestas mediante operaciones lógicas.

Las principales operaciones lógicas son: conjunción, disyunción, negación, condicional y Bicondicional.

A cada una de estas operaciones lógicas le corresponde una tabla de verdad.

p q	p Ù q
V V V F F V F F	V F F F

PROPOSICIONES COMPUESTAS:Una proposición lógica, compuesta por varias proposiciones representa das con
ley ras y unidas ente re sí con símbolos lógicos, que tenga la propiedad de que
cuando se reemplazan las ley ras por proposiciones reales siempre resulta
verdadera aunque algunas o todas esas proposiciones sean falsas, es lo que
se l lama una LEY LÓGICA.
Valor de verdad de la proposición compuesta " p  q " (p es equivalente a q)
Una equivalencia entre dos proposiciones es una proposición lógica compuesta que es
verdadera cuando las dos proposiciones tienen el mismo valor de verdad.
La Ley de la doble negación es una equivalencia que siempre es verdadera aunque la
proposición inicial sea falsa. Lo que esta ley dice es que siempre son equivalentes la doble
negación y la proposición inicial. Como ambas tienen siempre el mismo valor de verdad, la
equivalencia "(p)  p" es siempre verdadera y por eso es una ley lógica.

LOGICA PROPOSICIONAL

PROPOSICIÓN LÓGICA:

El valor de verdad de una proposición lógica atómica es, por definición, verdadero o falso (podemos representarlo como V o F).

Así el enunciado “llueve” es verdadero si y sólo si está lloviendo en ese momento. Pero si dicho enunciado se considera como proposición lógica atómica, p, entonces puede ser tanto verdadera como falsa.

Es una verdad de hecho o contingente, porque tiene los dos posibles valores de verdad, por la propia definición de proposición lógica.

El contenido de la relación de un enunciado con lo real no es objeto de la lógica sino de otras ciencias.