2.4 MAPAS DE KARNAUGH DE 5 VARIABLES

Recordemos que para conseguir el mapa de 5 variables, debe proyectarse el mapa de 4 variables. El abatimiento es hacia la derecha ya que el número de variables es impar. La figura adjunta muestra la proyección del mapa de 4 variables.

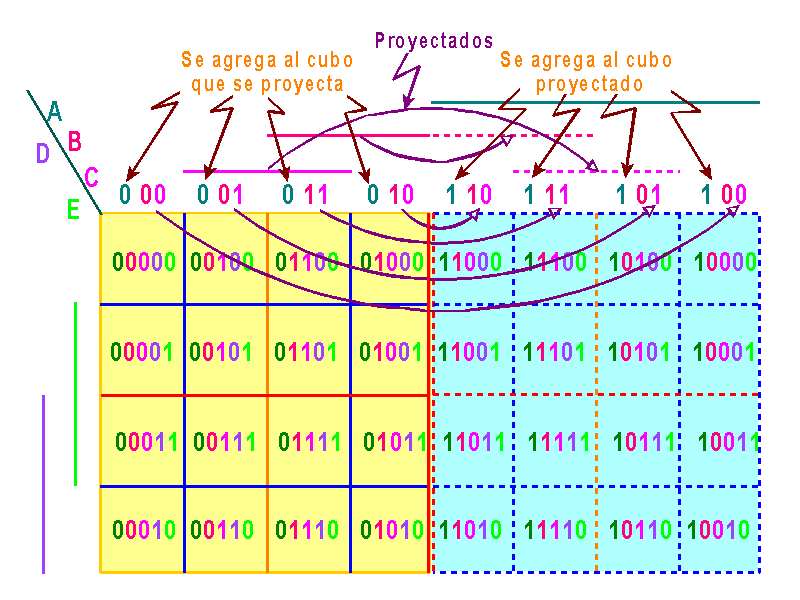
Obsérvese que al mapa que se proyecta se le antepone un 0 y al proyectado un 1. También, se ha asociado a cada celda el número binario correspondiente, el cual se obtuvo asignando el valor binario a cada variable en dicha celda.

Sustituyendo el número binario de cada celda por su equivalente decimal, se obtiene el mapa de Karnaugh para 5 variables que se empleará para minimizar funciones de conmutación de 5 variables independientes . La figura adjunta presenta este mapa.

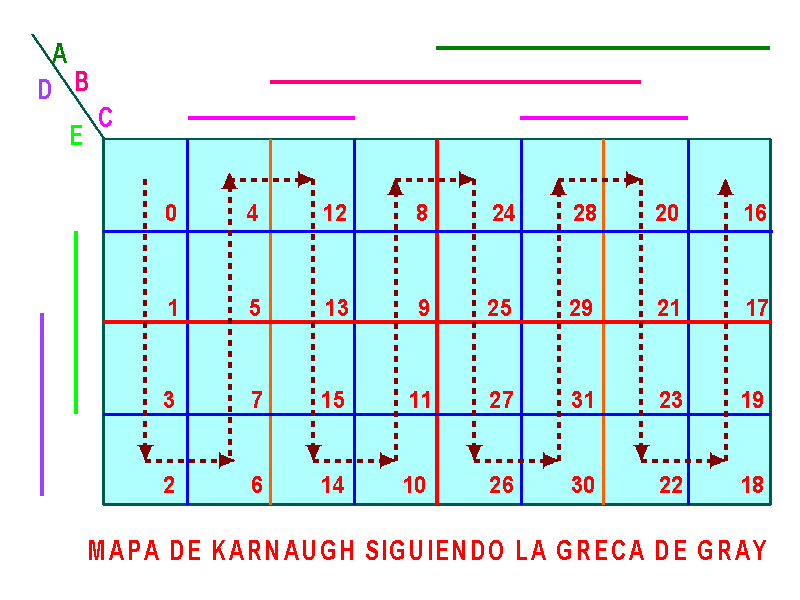
Para generar el código de Gray para 5 variables, se traza la greca de Gray sobre el mapa K para 5 variables y se escribe el código binario asociado a cada celda.

La figura adjunta muestra la greca de Gray sobre el mapa de Karnaugh de 5 variables.

A continuación se presentan algunos ejemplos que muestran la aplicación del mapa para la minimización de funciones de conmutación de 5 variables binarias.

EJEMPLO 6. Minimice las siguientes funciones, empleando el método de Karnaugh:

F1 = Sumaminitérminos (0,1,3,8,9,11,16-17,19,24,25,29-31)

F2 = Sumaminitérminos (0-4,6,9,10,15-20,22,23,25,26,31)

SOLUCION

Las siguientes figuras presentan los mapas K para F1 y F2: