domingo, 1 de agosto de 2010

Álgebra de Boole

De Wikipedia, la enciclopedia libre

Saltar a navegación, búsqueda

Álgebra de Boole (también llamada Retículas booleanas) en informática y matemática, es una estructura algebraica que rigorizan las operaciones lógicas Y, O y NO, así como el conjunto de operaciones unión, intersección y complemento.

Definición

El Álgebra de Boole es una estructura algebraica que puede ser considerada desde distintos puntos de vista matemático Como retículo

El álgebra de Boole es un retículo (A, 1,0, $\cdot$ , +), donde el conjunto A = {1,0}, como retículo presenta las siguientes propiedades, las leyes principales son estas:

1. Ley de Idempotencia:

$a \cdot a = a \,$

$a + a = a \,$

2. Ley de Asociatividad:

$a \cdot (b \cdot c) = (a \cdot b ) \cdot c\,$

$a + (b + c) = (a + b ) + c \,$

3. Ley de Conmutatividad:

$a \cdot b = b \cdot a \,$

$a + b = b + a \,$

4. Ley de Cancelativo

$(a \cdot b) + a = a \,$

$(a + b) \cdot a = a \,$

Como anillo

El Álgebra de Boole tiene Estructura algebraica de Anillo:

Grupo abeliano respecto a (+)

El conjunto A es un Grupo abeliano respecto a (+):

1. (+) es una operación interna en A:

$(a + b) \in A ; \; \forall a,b \in A \,$

2. Es asociativa:

$a + (b + c) = (a + b) + c ; \; \forall a,b,c \in A\,$

3. Tiene elemento neutro

$\exists 0 \in A ; \; \forall a \in A: a + 0 = 0 + a = a \,$

4. Tiene elemento simétrico:

$\forall a \in A; \; \exists \bar {a} \in A \; / \; a + \bar {a} = \bar {a} + a = 1 \,$

5. es conmutati Grupo abeliano respecto a (·)

El conjunto A es un Grupo abeliano respecto a ( $\cdot$ ):

6. ( $\cdot$ ) es una operación interna en A:

$(a \cdot b) \in A; \; \forall a,b \in A \,$

7. Es asociativa:

$a \cdot (b \cdot c) = (a \cdot b) \cdot c ; \; \forall a,b,c \in A\,$

8. Tiene elemento neutro

$\exists 1 \in A ; \; \forall a \in A: \; a \cdot 1 = 1 \cdot a = a \,$

9. Tiene elemento simétrico:

$\forall a \in A ; \; \exists \bar {a} \in A \; / \; a \cdot \bar {a} = \bar {a} \cdot a = 0 \,$

10. es conmutativa:

$a \cdot b = b \cdot a ; \; \forall a, b \in A$

El conjunto A={0,1} es un Grupo abeliano respecto a ( $\cdot$ ):

6. ( $\cdot$ ) es una operación interna en A:

$(a \cdot b) \in A; \; \forall a,b \in A \,$

7. Es asociativa:

$a \cdot (b \cdot c) = (a \cdot b) \cdot c ; \; \forall a,b,c \in A\,$

8. Tiene elemento neutro

$\exists 1 \in A ; \; \forall a \in A: \; a \cdot 1 = 1 \cdot a = a \,$

9. Tiene elemento simétrico:

$\forall a \in A ; \; \exists \bar {a} \in A \; / \; a \cdot \bar {a} = \bar {a} \cdot a = 0 \,$

10. es conmutativa:

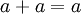
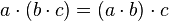
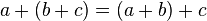
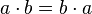
$a \cdot b = b \cdot a ; \; \forall a, b \in A$

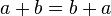
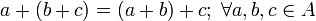
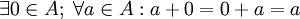
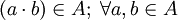
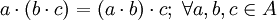
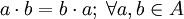
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)